Aberrations Panel
The Aberrations Panel is used to add aberration into the lens calculations.
Aberration Calculation Portion :
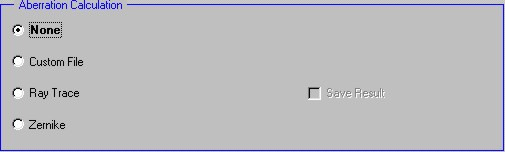
None
No aberration calculations are performed.
Custom File
The aberration data is loaded from the specified file. Here, opd1 contains the aberration data:

The aberration data should be stored in the project’s optics folder.
Ray Trace
Use a Ray Trace to calculate the aberrations. If the “Save Result” check box is checked, then the resulting aberration calculation is saved to the specified file.

Here, the Ray Trace calculation is stored in a file called opd1.mat:

The output of the ray trace calculation is stored in the project’s optics folder.
Zernike
Use the Zernike polynomial coefficients, which are found in the specified Zernike coefficient file, to calculate the aberrations. Here, the file zerndata.mat contains the required Zernike coefficients:

Zernike coefficient files should be stored in the project’s optics folder. The .mat file must contain the vector zvec. This file needs to be created before being able to use this function. To create it, first set up a zvec variable like the one in the example below. Afterwards use this command: save “filepath\filename” zvec. Remember that this should be in the project’s optics folder. The information box titled Zernike File should show the correct directory to save the file in. To edit the file just load it into the Matlab workspace and save it again.
zvec has the following format:
zvec(1) = order of the Zernike expansion.
zvec(2) = sampling in the pupil. This is the number of points across the pupil diameter that are used to calculate the initial Zernike distribution. The Zernike phase map resulting from the calculation will be resampled according to the sampling Npupil specified in the optics module, so it is recommended that zvec(2) be greater than Npupil.
zvec(3) through zvec(i) contain the Zernike coefficients as specified in Malacara, Optical Shop Testing.
Example:
zvec = [3 100 0 0 0 0 0 0 0 0 0.33 0];
This zvec produces a third-degree Zernike expansion that uses 100 points across the diameter of the pupil for the initial calculation. This particular choice of coefficients exhibits 1.0 wave of coma in the y direction with 0.33 waves of tilt.
Zernike Polynomials Unm Up to Fourth Degree
|
zvec(i) |
n |
m |
n-2m |
Zernike polynomial |
Monomial representation |
Meaning |
|
|
||||||
| zvec(3) | 0 | 0 | 0 | 1 | 1 | Constant Term |
|
|
||||||
| zvec(4) | 1 | 0 | 1 | ρsin(θ) | x | Tilt in x direction |
| zvec(5) | 1 | 1 | -1 | ρcos(θ) | y | Tilt in y direction |
|
|
||||||
| zvec(6) | 2 | 0 | 2 | ρ2sin2(θ) | 2xy | Astigmatism with axis at +/- 45 degrees |
| zvec(7) | 2 | 1 | 0 | 2ρ2-1 | -1 + 2y2 + 2×2 | Focus shift |
| zvec(8) | 2 | 2 | -2 | ρ2cos(2θ) | y2 – x2 | Astigmatism with axis at 0 or 90 degrees |
|
|
||||||
| zvec(9) | 3 | 0 | 3 | ρ3sin(3θ) | 3xy2 – x3 | – |
| zvec(10) | 3 | 1 | 1 | (3ρ3-2ρ)sin(θ) | -2y + 3xy2 + 3×3 | Third order coma along x axis |
| zvec(11) | 3 | 2 | -1 | (3ρ3-2ρ)cos(θ) | -2y + 3y3 + 3x2y | Third order coma along y axis |
| zvec(12) | 3 | 3 | -3 | ρ3cos(3θ) | y3 – 3x2y | – |
|
|
||||||
| zvec(13) | 4 | 0 | 4 | ρ4sin(4θ) | 4y3x – 4x3y | – |
| zvec(14) | 4 | 1 | 2 | (4ρ4-3ρ2)sin(2θ) | -6xy + 8y3x + 8x3y | – |
| zvec(15) | 4 | 2 | 0 | (6ρ4-6ρ2+1) | 1 – 6y2 – 6×2 + 6y4 + 12x2y2 + 6×4 | Third order spherical aberration |
| zvec(16) | 4 | 3 | -2 | (4ρ4-3ρ2)cos(2θ) | -3y2 + 3×2 + 4y4 – 4×4 | – |
| zvec(17) | 4 | 4 | -4 | ρ4cos(4θ) | y4 – 6x2y2 + x4 | – |

