Stork Data Errors
As described in Nature, there are systematic errors in the data in at least 12 of David Stork’s publications attacking the optical projection thesis that was put forward by David Hockney in his book Secret Knowledge, and by Hockney and me in six technical publications thus far. In every case the errors Stork has made with his data are such that they support the incorrect conclusions of those papers (after uncovering systematic errors in 12 of his papers, I ceased looking further, so the data in his other papers have yet to be examined). As an example of how glaring Stork’s errors are, below I show erroneous data in one of Stork’s papers, upon which he has based that paper’s incorrect conclusion. Click here for a summary of errors in nine of his other papers, and click here for a manuscript describing some of his errors in three other papers.
- Charles M. Falco
Did Georges de la Tour use optical projections while painting Christ in the carpenter’s studio?
David G. Stork
Ricoh Innovations
2882 Sand Hill Road Suite 115
Menlo Park, CA 94025-7054
and
Stanford University
Stanford, CA 94305
in, Human Vision and Electronic Imaging X
B. E. Rogowitz, T.N. Pappas, and S.J. Daly, editors
SPIE 566, 337 (2005)

I extracted Stork’s Figure 1 directly from the pdf file downloaded from his web page on the Stanford Psychology Department’s server on March 29, 2005 (as mentioned in Rex Dalton’s Nature article, after learning of these problems with his papers, in November Stanford removed his web page from their servers, but as of March 2, 2006 his web page and papers could be found on a server hosted by his collaborator Christopher Tyler). Figure 1 is exactly as extracted from his paper, except for the red notations added by me. Artifacts (dust spots, imperfections, resolution, etc.) show that the image Stork used for his analysis is identical to the jpeg of this painting located at Web Gallery of Art, which can be downloaded from there.
The violet dots connected by yellow lines are Stork’s data for this paper: “Figure 1 shows a number of straight lines linking the candle, the edge or corner of an opaque object, and its associated cast shadow. The lines show that these triplets are collinear, to excellent tolerance (less than a few angular degrees); these triplets are not consistent with a light source in the position of either of the subjects, as they would be, were Hockney’s claim correct.”
From his data, i.e. his ten violet data points that he connected with five yellow lines, Stork concludes that “We have shown compelling evidence that the illumination within Christ in the carpenter’s studio is due to the single candle held by Christ, and that source alone.” Stork’s analysis and conclusion that there is a single light source depends entirely on his data in Figure 1. However, there are serious problems with his data, a few of which are:
- Marked with a red “?” is a data point that Stork has placed on the shadow of the boy’s leg, precisely in the place it would have to be in order to be consistent with his conclusion of a single candle. However, there is no such kink in the image downloaded from Web Gallery of Art, or in either of the other two images of this painting that I located (see Appendix I below for a detail of this region);
- Stork placed a data point at the rear, left corner of the block of wood. However, his data point is significantly to the left of the actual location of this corner of the block. At the same time, he has placed the corresponding data point for its shadow too far to the right. In both cases, his errors are outside of the experimental uncertainty, with his combination of these two errors making his data consistent with his conclusion of a single light source. That is, the yellow line Stork draws between his two mis-plotted data points extrapolates to the candle. However, the red cone shown on this Figure, connecting the locations where these two data points actually should be plotted, differs by over 15 degrees from Stork’s line (note: the extent of the red cones in this figure represent my estimate of the range of experimental uncertainties for the locations of the actual data points; the data I used for this comparison are shown in Appendix I below);
- Stork has selectively omitted from his data set at least thirteen other distinct shadows — eleven of which I have marked with red ovals — that are needed to determine the number and locations of possible light sources. For example, the red cones I have drawn from the two omitted shadows that correspond to the front, right corner of the block can be seen to disagree with Stork’s conclusion. In fact, the mere existence of two shadows, both omitted by Stork from his data set, from a single corner shows that at least two light sources are represented.
- Stork has deceptively extrapolated the line between the boy’s toe and its shadow by a distance of nearly 20× to the precise point that supports his desired conclusion, even though such an extrapolation has a very large uncertainty.
In addition to being based on erroneous and selectively omitted data, another notable aspect of this paper is its false pretense of relevance to ‘the Hockney-Falco thesis.’ Stork has written a five-page paper attacking what is only a five-sentence aside by David Hockney in his book. On page 128 Hockney remarks that the two figures in this painting “were probably [emphasis added] painted separately, each lit by a shielded light source in place of the other figure.” It is clear from the book that this particular painting – one of over 150 paintings shown – is only peripheral to the optical thesis. Stork’s statement that he is attacking “a specific painting adduced as evidence for this bold theory” misleadingly pretends a significance for this painting, and hence for his five-page paper, that is absent even if Stork’s data were not erroneous.
Historical Context: de la Tour produced this painting in 1645, 220 years after the painting that contains our earliest scientific evidence of the direct use of optics (Robert Campin, Merode Altarpiece, c1425), 75 years after Cardano’s written description of how to use a convex lens to project images (1550), 36 years after Galileo sold an 8× telescope to the Venetian government (1609), and roughly contemporary with Vermeer’s extensively documented use of optical projections for his paintings (Philip Steadman, Vermeer’s Camera, Oxford, 2001). As such, this painting is one of scores of illustrations that Hockney used on his timeline of the later development of images. Clearly, though, from its relatively late date and the context of how Hockney used it in his book, it is almost insignificant by itself. Aside from everything else, given the extensive evidence that Vermeer was using optical projections as early as 1658, the claims Stork makes in his paper about the relevance of the 1645 de la Tour painting for disproving the Hockney-Falco theory are misguided at best.
To summarize, Stork has selectively omitted over 70% of the relevant data from this image (thirteen distinct shadows) that are needed to determine the number and locations of light sources represented. Of the five data pairs he does include, Stork has mis-plotted 40% of them (two out of the five lines) in the precise positions they would have to be in order to support his incorrect conclusion of a single light source.
Although I have shown errors in only one of David Stork’s papers here, his conclusions in at least 12 publications on this topic depend directly on data that are systematically in error in ways that in each case support the incorrect conclusions of those 12 publications.
Appendix I: Detail of Analysis
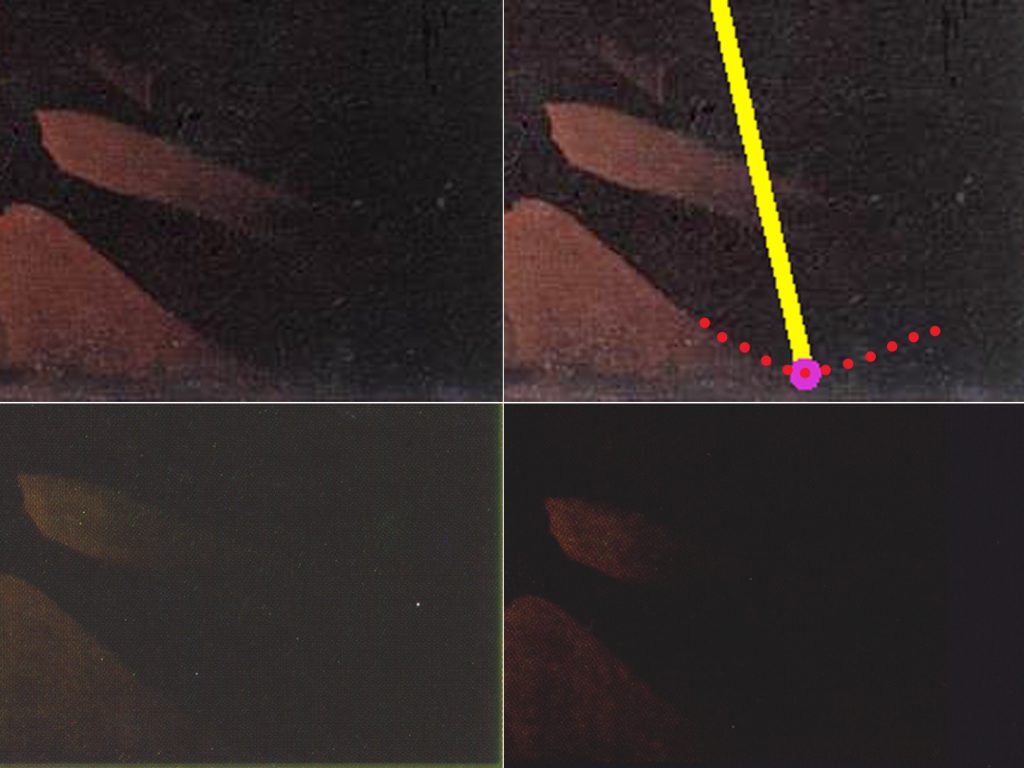
Detail from David Stork’s paper, with the dotted line showing where a kink in the shadow would have to be if Stork’s data point were correct (top right); jpeg downloaded from the Web Gallery of Art (top left); scanned from p. 128 of David Hockney’s Secret Knowledge (bottom right); and scanned from p. 416 of Lawrence Gowing’s Paintings in the Louvre (bottom left). In none of these images does the shadow exhibit a kink corresponding to the boy’s knee where Stork has placed his data point. Stork has placed this false data point in the precise location it would have to be in order to support his incorrect conclusion.

Detail from David Stork’s paper (right) and from the jpeg downloaded from the Web Gallery of Art (left). The red lines are the limits of my estimated uncertainties in locating three corners of the block and their corresponding shadows. The red cones I have placed over Stork’s Figure 1 fill in the spaces between these extrapolated lines for easier viewing, but it is the detail shown here that should be used for comparison with his data. Even a cursory examination reveals how far outside experimental error both of Stork’s data points are for the rear, left of the block. Also, aside from the other errors in Stork’s data, just the fact two shadows are apparent for the front, right corner of the block (both of which he selectively omitted from his analysis) shows that his statement that “We have shown compelling evidence that the illumination…is due to the single candle” is false.
After I pointed out in writing in 2005 that Stork’s data point for the kink in the shadow was false, he changed from the claim in his paper that it is a data point located “to excellent tolerance,” to instead having been meant only as “principled estimate.” He then wrote a paper justifying where he had placed that data point on the painting (“Mathematical Foundations for Quantifying Shape, Shading and Cast Shadows in Realist Master Drawings and Paintings,” SPIE 6314, 63150, 2006). That paper too is wrong.
Below is Figure 4 and its caption extracted from Stork’s 2006 paper. He has set up this scene to simulate the de al Tour painting in order to lead the reader to the conclusion that there must be a kink of the shadow of the boy’s knee just outside the painting, very close to where he had placed his data point in his 2005 paper. Stork writes in the caption that even though “the shadow of the tip” is not visible, “the direction toward the illuminant” can be determined. This is false. As I show in the red overlay, within the boundaries of this Figure the shadow cast by the marker would be the same no matter if the light source were anywhere within the semi-infinite plane extending arbitrarily far behind it. I also show two of the semi-infinite number of possible alternate locations for the light source, all of which would result in the same shadow. Just as with the de la Tour painting, without having the shadow’s tip (kink) within the image itself, it is impossible to extend lines backwards from an identifiable feature of the shadow, through the corresponding point of the object that cast it, in order to locate the position of the light source.

Figure and caption extracted from David Stork, SPIE 6314, 63150 (2006). I have overlaid two of the semi-infinite possible locations of the light source within a semi-infinite plane that would result in the same shadow being cast by the marker, and extended lines from them in the directions where the shadow’s tip would be in each case. Note that tip of the marker would not even be cast on the plane of the floor for the lower of the two possible light sources (it only would be seen if a wall were present).
Note that obviously there is no question where the tip in the shadow of this Figure must be, since it is a photograph captured in its entirety in ~1/60 sec. However, unless ade la Tour positioned all objects of the scene exactly as shown in his painting, and then somehow was able to project the scene in its entirety with a lens and capture it in 1/60 sec., before the boy moved his knee slightly, he got tired holding the candle and his arm sagged, the candle burned down, etc., only then would the light source and all of the shadows be positioned to the photographic accuracy Stork claimed to find with the data he reported in his 2005 paper. Clearly, Stork did not realize at the time he created his data points that, not only are they wrong, he positioned them far too precisely for them even to be reasonable.
Again, to summarize, of the semi-infinite number of locations where the kink in the shadow of the boy’s knee could be outside the borders of the de la Tour painting, Stork placed the data point in his 2005 paper in precisely the location inside the border of the painting where it would have to be to support his conclusion that “We have shown compelling evidence that the illumination within Christ in the carpenter’s studio is due to the single candle held by Christ, and that source alone.” After I pointed out in 2005 that this evidence was false, he then wrote another incorrect paper in 2006 attempting to justify what he had previously done as only an “estimate.” However, as the overlays on his Figure show, what he has done in this second paper is not even an estimate; it is wrong.
Appendix II: David Stork’s Fourteen Papers
On March 2, 2006 David Stork’s web page on Christopher Tyler’s server listed twelve publications on this topic, whereas earlier he had listed fourteen (Stork’s CV also changed on the Ricoh Innovations web page, where he is Chief Scientist, shortly after he was contacted by Rex Dalton of Nature early in February 2006: he deleted two of his four claimed ‘Editorial Boards’ listings, as well as all seven of the professional society memberships he had previously claimed). Following are the nine publications in which I found systematic data errors, all of which support the incorrect conclusions of those publications:
- David G. Stork, “Did Georges de la Tour use optical projections while painting Christ in the carpenter’s studio?” SPIE Electronic Imaging, SPIE 566, 337 (2005).
- David G. Stork, “Did Jan van Eyck build the first ‘photocopier’ in 1432?” SPIE Electronic Imaging Color Imaging IX: Processing, Hardcopy, and Applications, R. Eschbach and G. G. Marcu (eds.) pp. 50-56, 2004.
- Thomas Ketelsen, Olaf Simon, Ina Reiche, Silke Merchel, and David G. Stork, “Evidence for mechanical (not optical) copying and enlarging in Jan van Eyck’s Portrait of Niccolò Albergati,” Proceedings of the Optical Society of America Annual Meeting 2004. [although Ketelsen et. al are co-authors of this one-page publication, the data in it are in the form of a composite image that that is identical to one in Stork’s Scientific American article where he claims sole credit for having created it. An error of 2.6% that Stork made in creating his composite resulted in an apparent discrepancy that is consistent with his conclusion]
- David G. Stork, “Optics and realism in Renaissance art,” Scientific American, 291(6):76-84, December 2004.
- David G. Stork, “Optics and the Old Masters Revisited,” Optics and Photonics News, 15(3), pp. 30-37, March 2004.
- Antonio Criminisi and David G. Stork, “Did the great masters use optical projections while painting? Perspective comparison of paintings and photographs of Renaissance chandeliers,” in J. Kittler, M. Petrou and M. S. Nixon (eds.), Proceedings of the 17th International Conference on Pattern Recognition, Volume IV, pp. 645-648, 2004 (IEEE).
- David G. Stork, “Optics and realism in Renaissance art,” Scientific American, 291(6):76-84, December 2004.
- David G. Stork, “Were optical projections used in early Renaissance painting? A geometric vision analysis of Jan van Eyck’s ‘Arnolfini portrait’ and Robert Campin’s ‘Mérode Altarpiece’,” SPIE Electronic Imaging, Vision Geometry XII, L. J. Latecki, D. M. Mount and A. Y. Wu (eds), pp. 23-30, 2004.
- David G. Stork, “Asymmetry in ‘Lotto carpets’ and implications for Hockney’s optical projection theory,” SPIE Electronic Imaging, San Jose, January, 2005.
The journal IEEE MultiMedia published three additional papers during 2006/2006. Before the last of those three had gone to press one of the editors became aware of errors in them, resulting in an invitation for me to prepare a paper addressing Stork’s errors in those papers. Those three papers are:
- David G. Stork, “Computer Vision, Image Analysis, and Master Art: Part 1,” IEEE MultiMedia 13, no. 3, 13 (2006).
- David G. Stork and M.K. Johnson, “Computer Vision, Image Analysis, and Master Art: Part 2,” IEEE MultiMedia 13, no. 4, 12 (2006).
- David G. Stork and M.F. Duarte, “Computer Vision, Image Analysis, and Master Art: Part 3,” IEEE MultiMedia 14, no. 1, 14 (2007).
Three publications I have not yet examined for erroneous data are:
- David G. Stork, “Color and illumination in the Hockney theory: A critical evaluation,” Proceedings of the Color Imaging Conference (CIC11), Scottsdale AZ, November 2003, pp. 11-15.
- David G. Stork, “Did Hans Memling employ optical projections when painting ‘Flower still-life’?”, Leonardo 38, 57-62 (2005).
- David G. Stork, “Did early Renaissance painters trace optical projections? Evidence pro and con,” SPIE Electronic Imaging, Vision Geometry XII, L.J. Latecki, D.M. Mount, and A.Y Wu (eds.), pp. 25-31, 2005.
Missing from Stork’s list of publications on March 2, 2006 are two preprints that I have not examined for errors:
- Antonio Criminisi and David G. Stork, “Did the great masters trace optical projections? machine vision techniques address questions in art history,” 2004, submitted for publication.
- David G. Stork, “Did Caravaggio use optical projections when painting Supper at Emmaus?,” submitted for publication.

