Scientific and Technical Questions
Couldn’t all the “optical artifacts” you showed have been put there on purpose by the artists, without having used lenses?
No, it simply isn’t possible. Taking just one feature in Lorenzo Lotto’s ‘Husband and Wife’ as an example, the distorted octagonal pattern in the center of the table covering is reproduced to an accuracy of 2% by a precise octagonal pattern having been projected onto the canvas by a lens that had to be refocused twice at distances corresponding to the depth of field calculated for that lens. Each time Lotto refocused his lens the magnification of the projected image changed by an amount determined by the laws of geometrical optics. For this painting each of those changes in magnification is different, but both are within ±0.2% of the values calculated for them. The probability is vanishingly small that Lotto could have accidentally reproduced these complex features, and others, without having projected them with a lens. Ellen Winner, a psychology professor at Boston College, nicely made this point at a conference: “[Hockney and Falco] aren’t saying lenses are the only way to get the perspective right. They’re saying lenses are the only way to get the perspective wrong in precisely the ways these artists erred.”

(detail from Husband and Wife, Lorenzo Lotto, c1523)
Since we have published the details of our analysis of this painting, here I restate only our conclusions. The details can be found in: ETOP_OSA.pdf (Technical Digest of the Optical Society of America, 87th Annual Meeting (OSA, 2003).
Using only the measured magnification of this painting (0.56, i.e. roughly half life size, as determined from the size of the wife), the laws of geometrical optics uniquely determine both changes in magnification (–14.3% and –12.5%), the 3ochange in angle, the distance from the lens to the table covering (149.8 cm) and to the canvas (83.9 cm), as well as the focal length and diameter of the lens (53.8 cm and ~2½ cm, respectively) used to project this image. The three sets of vanishing points exhibited by the octagonal pattern, as well as the depths into the painting where they occur, are a direct and inevitable consequence of the use of a lens to project this portion of the painting.
[youtube id=”UZpECXv1JRc” mode=”normal” autoplay=”no” maxwidth=”850″]
1-minute clip by John Shadeck (M.A. student in art education) showing him reproducing the technique Hockney and I proposed Lotto used to create the central octagonal pattern on the carpet. As the clip shows, John used one lens from a pair of reading spectacles (2 diopter; focal length 50 cm) to focus the image of the symmetrical, octagonal pattern at the left onto his easel at the same magnification we calculated from the painting (0.56×). The small depth of field at this high magnification required John to refocus twice, resulting in a final pattern that reproduces Lotto’s to a remarkable degree.
Summary of Optical Evidence that Lorenzo Lotto Used a Lens or Concave Mirror:
Qualitative
- Octagonal pattern goes out of focus;
- Two sets of vanishing points are readily apparent in the octagonal pattern (closer inspection reveals a third set);
- Excellent fit of a perspective-corrected octagon to the pattern;
- Change to a 2nd vanishing point in the border is apparent at same depth into scene as octagonal pattern goes out of focus;
Quantitative
- The calculated –14.3% magnification decrease where the perspective of the octagonal pattern initially changes is within 0.2% of the value measured from the painting (calculated from equations for the depth of field + focal length);
- The calculated additional –12.5% magnification decrease where the perspective of the octagonal pattern changes again is within 0.2% of the value measured from the painting (from depth of field + focal length);
- An ideal perspective-corrected, three-segment octagon fits the octagonal pattern of the painting to within 2%;
- The calculated change in convergence of 3o is within 1% of that measured for the border pattern (from change in magnification upon refocusing + focal length);
- The 53.8 cm calculated focal length of the lens is quite reasonable (from magnification of painting);
- The ~2½ cm calculated diameter of the lens is quite reasonable (from depth of field).
What about vanishing points? They don’t seem to obey the laws of perspective in some of the paintings you have analyzed.
Actually, the vanishing points do obey the laws of perspective. It’s just that perspective, as taught in most elementary textbooks, is too simplified to be of use for analyzing imperfect, complex objects, like the chandelier in van Eyck’s ‘Arnolfini Marriage’ or the carpet in Lotto’s ‘Husband and Wife’. This is shown quite clearly by analyzing the photograph of a modern light fixture below.
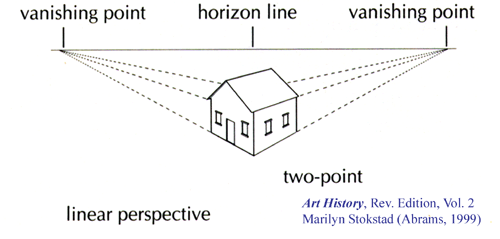
The above figure, taken from a widely-used art history textbook, shows that the lines from related features (in this case, each side of a house) all must come to a common focus, and that all of the foci must lie on a single horizon line. This is the common understanding of perspective as taught in nearly all textbooks. However, what these textbooks fail to mention is that it applies only to perfect, defect-free objects. Even very slight deviations from perfect symmetry result in lines deviating considerably from the idealized drawing shown in this figure. The next figure is the chandelier in van Eyck’s ‘Arnolfini Marriage’.

In the above figure I have carefully drawn lines through the six candleholders and extended them to see if they meet at a horizon line. Very clearly, they do not. Comparing this figure to the one from Stokstad’s textbook makes it seem the painting of the chandelier could not have been based on an image projected by a lens. However, a 15th century hand-made chandelier is a complex object that undoubtedly would have deviated at least slightly from perfect hexagonal symmetry. Because of this, attempting to “analyze” a painting like this by drawing lines through it tells us nothing one way or the other about whether or not the image is based on an optical projection. To repeat, only in the oversimplified version of perspective must the lines converge to foci, and the foci all lie on a single horizon line. That this is true can be clearly seen from the next Figure.

The above photograph is one I made of a 21st century chandelier on display at a store. Again, just as I did for van Eyck’s chandelier, I have carefully drawn lines through the six bulb holders. There is no question whatever that this image is in “perfect perspective,” because it is a photograph made with a modern lens. However, as is obvious, the lines neither converge to foci, nor to a single horizon line. In fact, the way the lines look on van Eyck’s painting and on the above photograph are remarkably similar, even though the chandeliers differ in age by nearly six centuries, and one is a painting and the other is a photograph. The overall diameter of this modern chandelier was 56 cm (~60% of the diameter I calculate for the Arnolfini chandelier), and the measured bulb-to-bulb distances between each of the six arms varied by a maximum of only 0.95 cm. That is, manufacturing tolerances of no better than ~1 cm for a chandelier of this size are all that are needed for it to look perfect to an observer, while at the same time resulting in perspective lines that vary as much as they do for the Arnolfini chandelier.
In the second figure of this section I showed the simplistic, incorrect way to attempt to analyze the perspective of the Arnolfini chandelier by drawing lines through it. However, it is possible to do even worse than just the drawing of lines if one does not understand perspective; compounding one fundamental error with an additional one.

Immediately above is a detail from the Arnolfini chandelier. Even if one has only an elementary understanding of metal working, it should be clear that the decorative features above and below each of the six main arms of the chandelier would have been fabricated separately and then hand-attached (by soldering or riveting), so they would inevitably vary somewhat in relative position from one arm to the next. Because the arms are so close together, even if the arms themselves exhibited perfect hexagonal symmetry (which, of course, they would not, because the chandelier was an object made by hand in the 15th century), minor variations of only a few millimeters in the attachment of such features to the arms would result in significant deviations in the slopes of lines drawn through them, and thus where those lines ended up when extrapolated a considerable distance in the vain hope of finding vanishing points. Hence, to use such hand-attached decorative features in any sort of perspective analysis would be quite naive.
To summarize, optical perspective as taught in elementary textbooks is shown in the first figure of this section. This simplistic version of perspective implies that an image can be analyzed to determine if it was based on an optical projection by drawing lines, that in turn must converge to precise vanishing points, all of which must lie on a horizon line. However, what I showed with the other figures in this section that this will lead to the wrong conclusion if such an oversimplified scheme is applied to a photograph of even a slightly imperfect complex object like a light fixture, let alone to a painting that has additional deviations introduced by the artist. The table covering in Lorenzo Lotto’s ‘Husband and Wife’ presents an even more complex perspective problem because, as we have previously shown (Optics and Photonics News, July 2000), the artist had to move his lens twice when he exceeded its depth of field, resulting in three sets of projections. However, this problem is still quite tractable (although, not by simply drawing lines). A full discussion of both van Eyck’s chandelier and Lorenzo Lotto’s table covering can be found in: ETOP_OSA.pdf (Technical Digest of the Optical Society of America, 87th Annual Meeting (OSA, 2003)
How can you say people don’t know about ‘mirror lenses’ when surely everyone knows about reflecting telescopes?
Unfortunately, my experience has been that only a very small number of non-scientists realize that reflecting telescopes form images in the same way that concave mirrors (‘mirror lenses’) do. Although in recent years several major photographic equipment manufacturers (Minolta, Nikon, Sigma, and Vivitar) have sold telephoto lenses based on concave mirrors, those lenses also contain a few conventional refractive glass elements to reduce residual aberrations, so perhaps the presence of the additional glass causes people not to realize their principle of operation.
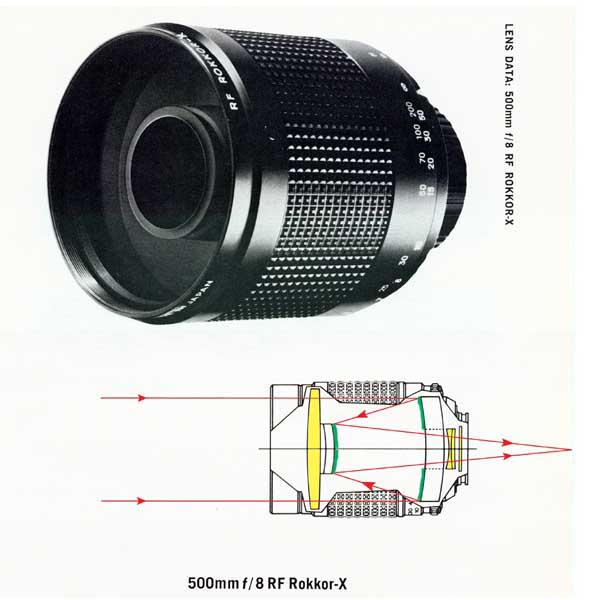
The key component in this Minolta 500 mm focal length lens is the concave mirror toward the right side of the cutaway diagram, with its reflective coating shown in green on the front of the concave surface. Although only that one mirror is required in order to form an image, that image would be located outside the camera rather than on the film. Hence, a second (convex) mirror is used to reflect the light rays back into the camera itself. Several conventional refractive glass elements, shown in yellow, are also included in this lens design to reduce aberrations from the spherical mirror surfaces. However, they are present only because this lens is for 35 mm photography, where the small image on the film (24×36mm / 1″×1.5″) has to be of sufficient quality to allow subsequent magnification by at least 10× when making prints for viewing. Because of the large glass optical element at the entrance to the lens many people may not realize that, in essence, this type of lens works by means of the internal mirrors alone, with the refractive elements there only to “fine tune” the final image.
Where does the camera obscura fit into your explanation?
[note: physicists use the Latin obscura while art historians often use the Italian oscura]
This term has been the source of considerable confusion, since the word “camera” brings to mind the modern use of the word. Certainly such modern-looking boxes did exist by the 17th century and were used by some painters. However, the literal translation of camera obscura, “dark room,” is how it should be thought of. The room (“camera”) can be of any size, from a portable box, to an entire room of a house.

If you cover the window of your bathroom with a heavy black cloth and punch a hole in it of diameter roughly ¼”, an image of the outdoors will be projected upside down onto the opposite wall. An image that is both brighter and sharper can be focused onto a surface within your room by substituting an actual lens (or, in a slightly different configuration, a concave mirror) for the “pinhole.” Hence, anyone troubled by the lack of an explicit entry for “camera obscura” on a detailed inventory of an artist’s estate should realize that to have had one the artist would have needed to posses nothing more than some cloth and an inconspicuous lens.
On Vermeer’s possible use of a camera obscura, Tomaso da Modena’s 1351 paintings discussed elsewhere in this FAQ show that inexpensive optics of the necessary quality to substitute for the pinhole had been available in Europe for 300 years prior to Vermeer’s time. Also, the microscope manufacturer Antony van Leeuwenhoek was executor of Vermeer’s will, providing a direct connection to the imaging world. In his book Vermeer’s Camera (Oxford, 2001), Philip Steadman provides a compelling case based on his analysis of the paintings that, indeed, Vermeer did use a camera obscura. The requisite evidence that Vermeer used a lens as a tool to aid his painting is within the images themselves.
Can you reproduce these effects with a modern camera and lens? If so, can you give me the details so I can do it myself?
Yes, you certainly can use modern cameras to reproduce all the “optical” effects we have discovered. In fact, I did so in the course of my work in order to independently verify all of the calculations I had made, as well as to gain additional insight into other possible optical effects to look for in paintings. However, because of the autofocus feature of nearly every modern camera, combined with their limited close-focus distance (and, hence, limited magnification), realistically it requires a specialty camera with a manual focus “macro” lens to easily reproduce the effects. Refer to the two photography books listed in Further Reading for details on the features inherent to images projected at high magnification.
I tried to project an image myself with a concave mirror and it seemed fairly dim; how much light is required?
A precise answer to this question depends on knowing the magnification of the image as well as the diameter of the mirror, since in both cases the brightness scales as the square of the quantity. However, unless you are using a mirror smaller than an inch in diameter, or are trying to project an unusually large image (e.g., one larger than life size), direct sunlight on the subject should result in a quite bright image if you have things arranged correctly. For setups configured as our estimates show they were assembled by Campin, Caravaggio, Lotto, etc., it turns out that the projected image of a subject who is standing in direct sunlight is roughly as bright as if, instead, you look directly at the same subject standing in the light coming from a north window. That is, the projected image has ample brightness. The photographs on page 76 of Hockney’s book, as well as the next (and the previous) movie clip in this FAQ, show that the brightness of projected images isn’t a problem. For example, the upper left photo on on page 76 of shows that David, illuminated only by the indirect light coming through the window, is roughly the same brightness as the projected image he is working with. Hence, if there were a second artist in that room, he or she would have had ample light to paint a portrait of either David or of the projected image with equal ease.
[youtube id=”oG_Ac-8YDX4″ mode=”normal” autoplay=”no” maxwidth=”850″]
This clip shows the brightness and amazing detail of an image projected with a home made concave mirror. The previous clip also shows how bright the image is.

