Acoustoelectrically enhanced optomechanical interactions

The acoustoelectric effect allows dynamic reconfigurability of phonon loss in a medium. Control over this typically static parameter opens up a range of new and exciting possibilities in acoustic wave physics, including but not limited to Brillouin scattering. Brillouin Scattering is a nonlinear optical process in which light of a given frequency interacts with an acoustic wave to produce light of another frequency. This nonlinear process has become the basis for a variety of optical signal processing technologies such as: filters, delay lines, lasers, amplifiers, and nonreciprocal devices.[1] There are two types of Brillouin scattering processes: Stokes and anti-Stokes. In a Stokes scattering event, a photon from the input (or pump) beam is scattered to a lower frequency photon and a generates an acoustic phonon in the process. The difference in energy between the pump photon and output photon is equal to the energy of the phonon (i.e., the energy of the input particle is equal to the sum of the energy of the two output particles). In an anti- Stokes scattering event, a lower frequency photon and an acoustic phonon combine to produce a higher frequency photon. Here the sum of the energy of the two input particles is equal to the energy of the output particle. The conservation of energy in both these processes can be expressed by the equations below.

{"aid":null,"backgroundColor":"#FFFFFF","id":"10","font":{"size":18,"family":"Arial","color":"#595959"},"code":"$$\\omega_{s}=\\omega_{p}-\\Omega\\,\\,\\,\\,\\,\\,\\,\\,\\,\\,\\,\\,w_{as}\\,=\\,w_{p}\\,+\\,\\Omega$$","type":"$$","ts":1696022198768,"cs":"lbpjLostbbwp5wuWgu8sMw==","size":{"width":388.3333333333333,"height":28}}


Where ωp, ωs, ωas represent the angular frequency of the pump, Stokes, and anti-Stokes beams, respectively, and Ω represents the angular frequency of the acousticbeam. More information about Brillouin scattering and other nonlinear processescan be found in the introductory text by Boyd.[2] However without going through the detailed derivation, one can imagine that the gain of a Brillouin process is heavilyinfluenced by the amount of power in each of the beams involved. Furthermore, wecan imagine that the rate at which the power is lost (or dissipated from the system) affects the efficiency of the scattering process.

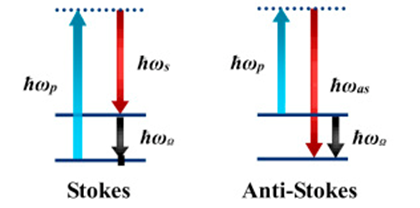
The above diagram shows the two types of Brillouin scattering events. In the Stokes case a higher energy pump photon is annihilated, generating a lower energy Stokes photon and a phonon. In the anti-Stokes case a lower energy photon and a phonon are annihilated, generating a higher energy anti-Stokes photo.

Because of Brillouin scattering’s dependence on power dissipation, the ability to dynamically reconfigure phonon loss is highly desirable. The acoustoelectric effect allows for just that­.[3] This effect leverages the Coulombic drag experienced by acoustic waves in piezoelectric media to introduce acoustic gain via the input of electrical energy. Acoustoelectric amplification has been a topic of discussion since the early 1970s. [4] However, the maturation of micro-fabrication technology has recently turned these ideas into a reality. Control over an acoustic system’s dissipation rate opens up a range of exotic solutions for miniaturization in RF signal processing as well as new physical regimes and significant performance enhancement in Brillouin scattering based devices.[5]

The above diagram shows the relationship between applied drift field and acoustoelectric phonon gain, as well as the different accessible scattering regimes in an acoustoelectric Brillouin device. Traditional devices operate at zero drift field, which results in slightly negative phonon gain (loss).
Illustration of a stimulated Brillouin scattering waveguide. The pump and Stokes waves (Ap and As, respectively) are coupled into the waveguide via grating couplers. The beating of these two counter-propagating waves produces an acoustic wave which is amplified by the acoustoelectric effect in the region between the two gold electrodes. Pump photons are then inelastically scattered off this acoustic energy into Stokes photons.

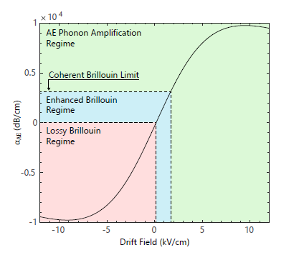
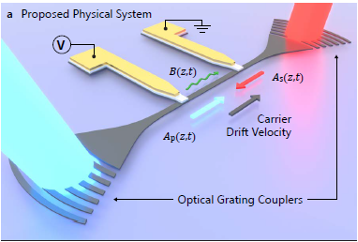
References

  1. B.J. Eggleton, C.G. Poulton, P.T. Rakich, et al., “Brillouin integrated photonics,” Nat. Photonics, vol. 13, pp. 664-677, 2019. [Online]. Available: https://doi.org/10.1038/s41566-019-0498-z
  2. R.W. Boyd, Nonlinear Optics, 3rd ed. San Diego, CA: Academic Press, 2008.
  3. L. Hackett, M. Miller, F. Brimigion, et al., “Towards single-chip radiofrequency signal processing via acoustoelectric electron–phonon interactions,” Nat. Commun., vol. 12, no. 1, p. 2769, 2021. [Online]. Available: https://doi.org/10.1038/s41467-021-22935-1
  4. G.S. Kino and T.M. Reeder, “A Normal Mode Theory for the Rayleigh Wave Amplifier,” IEEE Trans. Electron Devices, vol. 18, no. 10, pp. 909-920, Oct. 1971. [Online]. Available: https://doi.org/10.1109/T-ED.1971.17304
  5. N.T. Otterstrom, M.J. Storey, R.O. Behunin, L. Hackett, P.T. Rakich, and M. Eichenfield, “Modulation of Brillouin Optomechanical Interactions via Acoustoelectric Phonon-Electron Coupling,” Phys. Rev. Appl., vol. 19, no. 1, p. 014059, Jan. 2023. [Online]. Available: https://doi.org/10.1103/PhysRevApplied.19.014059