Collective Spin Squeezing Lab
In the Jessen research group, we are developing tools for quantum control and quantum measurement of collective spin systems. As our basic physical platform, we use the collective spin of a cloud of trapped Cesium atoms, coupled to a probe beam of laser light. The strength of the spin-probe coupling can be characterized by the amount we learn about the spin by measuring the probe light. If the coupling is strong enough, such a measurement gives sufficient information about the spin to cause quantum back-action. In our case, quantum back-action can be observed in the form of spin squeezing.
Let us take these concepts one at a time. First, quantum back-action is the change in the quantum state that results when some property of a physical system is measured with a precision below the quantum uncertainty of the corresponding observable. Consider, for example, a cloud of atoms with a collective spin aligned along the x-axis (Figure 1).
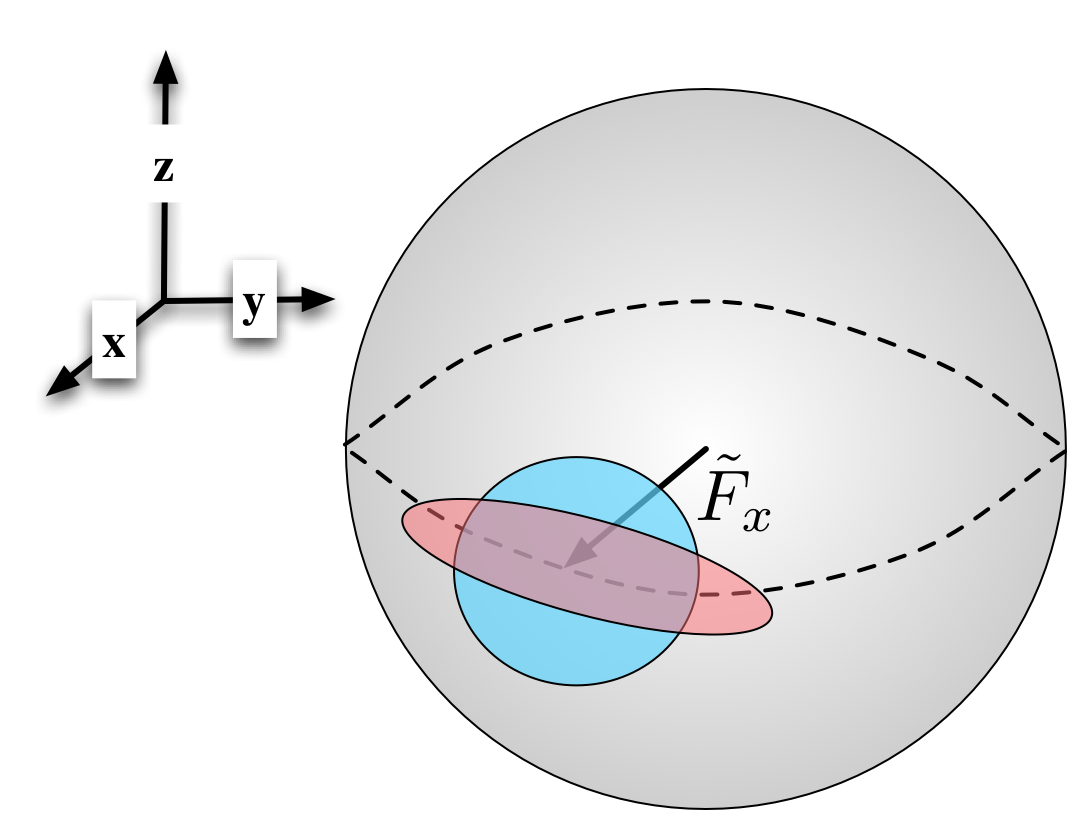
Fig. 1. Depiction of the Bloch sphere for the collective spin of an ensemble of atoms. Because the collective spin is aligned along the x-axis, the average value of repeated measurements of the z-component of the spin will be zero. However, the uncertainty principle causes the value of individual measurements to fluctuate about this average value (blue, circular uncertainty spot). Improved knowledge of the value of the z-component is possible (spin squeezing), but only at the expense of knowledge in the orthogonal y-component (red, elliptical uncertainty spot)
In this case, measurements of the z-component of the spin will, on average, give a value of zero. However, the actual value of individual measurements will fluctuate because of the uncertainty principle, which in this case requires that the product of uncertainties along the y- and z-axes, respectively, obey the inequality
![]()
The quantum uncertainty manifested by the fluctuations can be reduced via a measurement that increases our knowledge of the spin component along the z-axis, though at the cost of decreasing our knowledge (increasing the quantum uncertainty) of the spin component along the y-axis. This is precisely the condition known as spin squeezing. In our experiment, a non-zero spin component along the z-axis leads to Faraday rotation of the probe polarization, and this rotation can be detected with a polarimeter. In practice, the challenge is to increase the spin-probe coupling enough that quantum fluctuations of the spin cause fluctuations in the Faraday rotation that are large enough to be visible above the photon shot noise of the probe. Under these conditions, an indirect measurement of the spin, via its effect on the probe, leads to quantum back-action and spin squeezing.
The basic idea of producing spin squeezing via quantum measurement can be extended in several ways. With our collaborators in the theory group of Prof. Ivan Deutsch at the University of New Mexico, we have explored a promising scheme based on quantum coherent feedback, where the probe beam interacts with the collective spin during two consecutive passes through the atom cloud [1]. The first pass leads to Faraday rotation of the probe polarization proportional to the spin component, Fz. This polarization rotation is converted into ellipticity, with the result that the probe, during its second pass, acts on the collective spin as a fictitious magnetic field proportional to Fz. The ensuing rotation of the spin around the z-axis by an amount proportional to its z-component is a well-known mechanism for the generation of spin squeezing [2]. Additional refinements are required to eliminate residual spin-probe entanglement and to “phase-match” the squeezing interaction. If successfully implemented, this scheme can, in principle, produce far greater spin squeezing than the measurement-based approach.
We are currently pursuing two separate experimental approaches to produce strong coupling between the collective spin of a trapped atom sample and an optical probe beam.
Dipole Trap
The first approach will generate a trapping potential with focused laser beams propagating through free space (Figure 2).
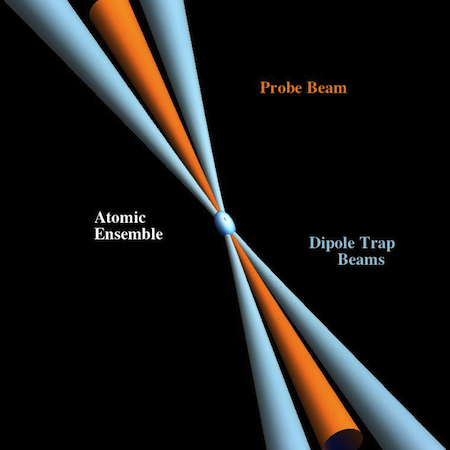
Fig. 2. Illustration of atoms trapped at the focus of two intersecting laser beams. This optical dipole trap relies on the dipole interaction of the atoms with the red-detuned laser light to attract atoms to the high intensity region of the beams. Changing the angle between the beams or the amount of power from the laser allows us to control the shape of the trapping region and consequently, to pick the trap shape that will create the strongest coupling between the atoms and the incoming probe beam
Loading a few hundred thousand atoms into this optical dipole force trap [3] will produce a cloud with an effective optical depth of 50 or more on-resonance (the requirement for strong coupling is equivalent to
![]()
Optical Nanofibers
The second approach takes advantage of new developments in atom trapping with optical nanofibers [4]. Here, a regular optical fiber is tapered to a thickness of only 500 nm, such that light propagating through the nanofiber region has a substantial evanescent field extending into the vacuum surrounding the glass core (Figure 3).
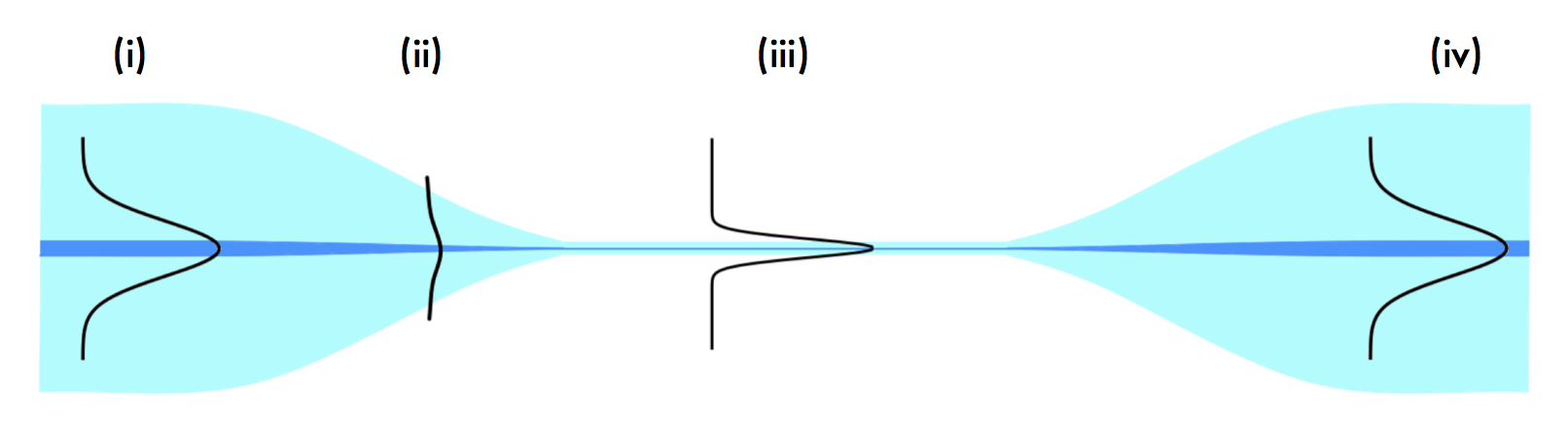
Fig. 3. Cartoon representation of light traveling through a tapered optical nanofiber (not to scale). Before the tapered region (i), the fiber consists of a core of order 10 micrometers and a cladding of about 100 micrometers. In this section, light propagates primarily through the core, with evanescent waves traveling in the cladding of the fiber. As the optical nanofiber tapers (ii), the core begins to disappear and more laser power travels in the cladding of the fiber. Then, in the narrowest section (iii), the core disappears entirely, and the cladding carries much of the power. The evanescent waves, however, travel entirely outside of the optical nanofiber because the wavelength of the light propagating through the fiber (780 – 1064 nm) is greater than the 500 nanometer width of the fiber. Finally, as the taper reverses itself (iv), the light re-enters the core and propagates as in section (i)
Vetsch et al. [4] have demonstrated that atoms can be trapped in this evanescent field and coupled to a probe beam propagating through the nanofiber. Extrapolating from their work, it appears that optical depths of more than 100 should be possible with just a few thousand trapped atoms. We are now setting up a nanofiber experiment using nanofibers (Figure 4) provided by the group of Prof. Arno Rauschenbeutel at Vienna Technical University.
Successful development of the above tools for quantum control and measurement will have applications to quantum metrology and to the development of atom-light quantum interfaces. From the perspective of quantum information science, quantum coherent control of the collective spin of an ensemble opens the door to further studies of non-linear Hamiltonian dynamics [5], quantum chaos [6], and many-body physics [7].
[1] Collin M. Trail, Poul S. Jessen, and Ivan H. Deutsch, Phys. Rev. Lett. 105, 193602 (2010).
[2] M. Takeuchi, S. Ichihara, T. Takano, M. Kumakura, T. Yabuzaki, and Y. Takahashi, Phys. Rev. Lett. 94, 023003 (2005).
[3] R. Grimm, M. Weidemüller, and Y. Ovchinnokov, Adv. Atom. Mol. Opt. Phys. 42, 95 (2000).
[4] E. Vetsch, D. Reitz, G. Sagué, R. Schmidt, S. T. Dawkins, and A. Rauschenbeutel, Phys. Rev. Lett. 104, 203603 (2010).
[5] G. A. Smith, S. Chaudhury, A. Silberfarb, I. H. Deutsch, and P. S. Jessen, Phys. Rev. Lett. 93, 163602 (2004).
[6] S. Chaudhury, A. Smith, B. E. Anderson, S. Ghose, and P. S. Jessen, Nature 461, 768 (2009).
[7] I. Bloch, J. Dalibard, and W. Zwerger, Rev. Mod. Phys. 80, 885 (2008).

