Brain Teasers
Week of January 12
Make four identical equilateral triangles using only six matches. (You are not allowed to break the matches, and the number of triangles should not exceed four.)
Week of January 19
One hundred light bulbs are arranged in a row and numbered sequentially, from 1 to 100. Each bulb has a toggle-switch that is used to turn it on when it is off, and vice versa. Starting with the first bulb, we turn them all on. We then move to the second bulb and toggle all bulbs identified by an integer-multiple of 2 to the off state. Next we move to the third bulb and toggle the state of all bulbs whose numbers are multiples of 3, and so on. This process continues until we reach the last bulb in the row. Which light bulbs will be on at the end?
Week of January 26
1) A small boat sits in the middle of a pool. A large rock is in the boat. If the rock is thrown into the pool, does the water level rise, fall, or remain the same?
2) If you have a clock on which the hour and minute hands are identical, will there be any times that are ambiguous (along the lines of 1:21 and 4:07, say), and if so, how many?
Week of February 2
A wine bottle has just been uncorked. You are handed the bottle, the cork, a large wineglass, and a marker with which to write on the bottle. You are asked to pour exactly half of the wine into the glass. How would you go about it?
Week of February 9
A short piece of rope is known to take exactly one hour to burn from one end to the other, but the burn rate is uneven. Given two such pieces of rope and a cigarette lighter, how does one go about measuring a 45 minute interval?
Week of February 16
In this infinite network of identical pairs of resistors R1 and R2, what is the resistance between A and B?
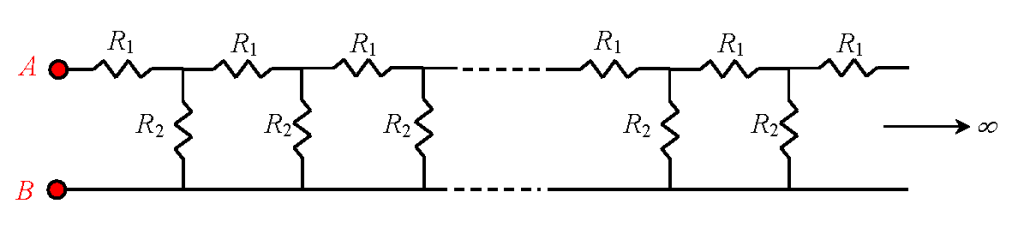
Week of February 23
In this infinite network of identical resistors, what is the resistance between A and B?
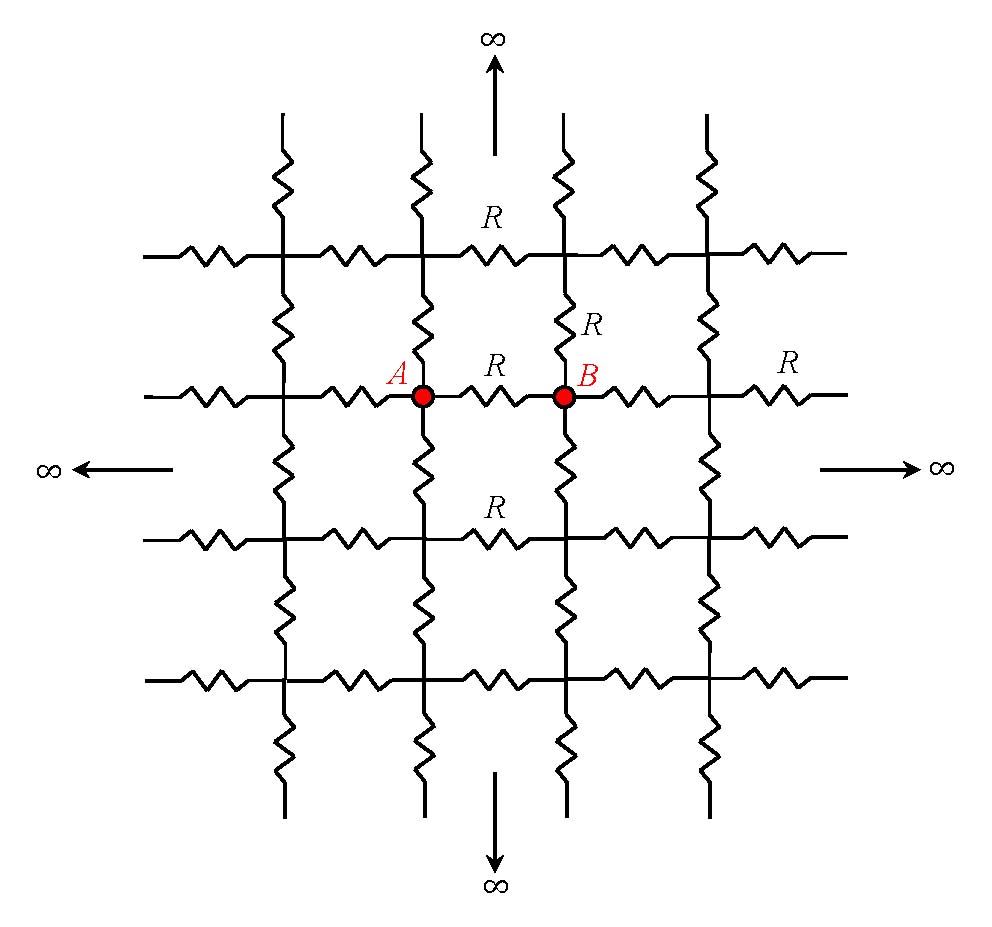
Week of March 2
1) A narrow trail leads from a monastery at the base of a mountain to a temple at the mountaintop. A monk sets out from the monastery one day at dawn, walks up the trail at an uneven pace, reaching the temple at dusk. He spends the night at the temple, then leaves early morning the next day and returns to the monastery by sunset. Show that there is one point along the trail where the monk has been at that point at precisely the same time on both days.
2) A game-show contestant is shown three closed doors to choose from. He is told that an expensive car awaits him behind one of the doors, whereas a goat lurks behind each of the remaining doors. The contestant will have to choose a door, and his prize will be whatever happens to be behind the door. Once the contestant announces his choice, the host opens one of the other two doors to reveal a goat behind it. She then asks the contestant if he would like to switch his choice to the remaining door. Now, the contestant’s chances of winning at first were one out of three. However, after the host opened one of the doors and revealed a goat behind it, his chances of winning would double (i.e., become two out of three) if indeed he chose to switch. Explain the rationale behind this increased chance of winning.
Week of March 16
A staircase has 100 steps. Standing on each step is a man wearing either a white or a black hat. None of the men knows the color of his own hat. All the men are facing downstairs, so that the man on the highest step can see the colors of the hats on the 99 men below him. Similarly, the man on the 99th step can see the colors of the 98 hats below him, and so on. Before the game begins, the men are allowed to strategize among themselves. Once the game is started, each man is expected to guess the color of his own hat, then announce it in a loud and clear voice that the other men can hear. What strategy should the men employ to maximize the total number of their correct guesses?
Week of March 23
1) Continue the following sequence: O T T F F S S E N T E T T . . . .
2) 200 ants are placed randomly at various points along a one-meter-long rod. The ants move on a straight line along the length of the rod at a constant speed of 1.0 cm/sec. When two ants collide, they turn around and move in the opposite direction (at the same speed). Ants reaching either end of the rod fall off the edge, never to return. How long does it take for all the ants to fall off?
Week of March 30
Thirteen highly-intelligent men are incarcerated in the same jailhouse. The prisoners may observe each other, but are forbidden to communicate by direct or indirect means. Shortly after noon one day, the jail keeper places either a red mark or a green mark on each man’s forehead, without informing him of the color of the mark. Each prisoner can see the faces of all the others, but cannot see his own. The jail keeper then informs the prisoners that those with a green mark are free to leave provided that they determine (using pure logic) that they have received a green mark. There will be severe punishment if a red-marked prisoner attempts to leave. Following this announcement, the guards open the door once every hour at the hour, for a few seconds each time, so the green-marked prisoners may exit. Nothing happens until 7:00pm that night, at which point all seven men who have received the green marks get up and leave. How did they recognize the color of their mark, and why did it take them so long?
Week of April 6
A teacher walks into a classroom where 50 students are sitting at their desks. The students know each other well, but the teacher knows nothing about them except that one student is a truth-teller while the remaining 49 are togglers. (A toggler is someone who alternates between lying and telling the truth. If he gave the correct answer to your first question, he would lie in response to the second, and vice versa. It is not known whether a toggler’s first answer is true or false, but if you posed two questions, you are assured of the veracity of exactly one of his two answers.) The teacher is allowed to ask two questions. She may ask both questions from the same student, or direct each of her questions to a different student. How does she find the truth-teller?
Week of April 13
1) Without lifting the pen from the paper, connect these nine dots using four straight lines.

 2) One hundred passengers, each with an assigned seat, board a plane that has exactly one hundred seats. The first passenger, ignoring his or her seat assignment, chooses one of the available seats at random. The remaining passengers, upon boarding the plane, sit on their assigned seats, unless the seat has already been occupied, in which case they choose, again randomly, one of the available seats. What is the probability that the last passenger, upon boarding, will find his or her assigned seat still available?
2) One hundred passengers, each with an assigned seat, board a plane that has exactly one hundred seats. The first passenger, ignoring his or her seat assignment, chooses one of the available seats at random. The remaining passengers, upon boarding the plane, sit on their assigned seats, unless the seat has already been occupied, in which case they choose, again randomly, one of the available seats. What is the probability that the last passenger, upon boarding, will find his or her assigned seat still available?Week of April 20
There exist a total of 25 horses and you are allowed to race only 5 horses at a time. Each race determines the relative speeds of the five horses involved, but not their absolute speeds. How many races are needed to find the three fastest horses.
Week of April 27
A rectangular piece is cut out of a round cake, leaving a rectangular hole behind. The hole and the cake are not concentric. Describe a single straight cut that would split the remaining cake into two equal halves. (The trivial solution of cutting parallel to the surface is not allowed.) This problem can be generalized to shapes other than circle and rectangle for the cake as well as the hole. Allowed shapes (for both the cake and the hole) are circle, ellipse, hexagon, rectangle, and parallelogram. Shapes that are not allowed include triangle, trapezoid, and pentagon.
Week of May 4
Stand in front of a large, flat mirror, and see your image staring back at you. The image represents your appearance in just about every respect, except for a few subtle differences, such as your right hand becoming the image’s left hand, and vice versa. Of course, there is nothing special about the left-right symmetry of the mirror that differs from its up-down symmetry. Why is it then that your head and feet do not switch places in the mirror?
